Hess's Energy Cycle

Enthalpy changes using combustion data

• Many enthalpy changes of formation reactions do not occur under standard conditions, and so they cannot be directly measured; however they can be measured indirectly using energy cycles.
• Elements react to form a compound. When the compound is combusted it forms the same substances as when the elements are combusted. Using this relationship we can work out the standard enthalpy of formation indirectly.

∆H_c1= ∆H_f + ∆H_c2

• The total enthalpy of combustion for the reactants is equal to the formation energy of the products plus the combustion energy of the products. 
• This makes sense as Energy can neither be created nor destroyed, so as long as the starting point and the finishing point are the same, then the enthalpy change will always be the same no matter how you get from start to finish.
• So if a process can be written in several steps, the enthalpy change of the whole process is equal to the sum of the steps.

To find out the Enthalpy change using Heats of combustion:

• Start with an equation to represent the energy change.
• Using the combustion data complete a Hess law cycle.
• Balance the cycle and add symbols representing ∆H₁ ∆H₂ and ∆H_3.
• Remember to get the direction of change correct (arrows go form reactants and products down to the combustion products).
• Use Hess's law to find the relationships between the enthalpy changes and rearrange to find the value wanted.

Example:

Find the Enthalpy Formation Energy of Methane.

•   So, if we can measure ∆H_c2 and ∆H_c1, we can work out ∆H_f.

∆H_f = ∆H_c2 - ∆H_c1

• It is minus ∆Hc₁ because the reaction is going in the opposite direction to what we want.
•        ∆H_c2 is the sum of enthalpy changes of combustion of 1 mole of carbon and 2 moles of hydrogen and ∆Hc₁ is the enthalpy change of combustion for methane, and ∆H_f is the enthalpy change of formation for methane, which is what we are trying to find out.

∆H_{f =} ∆H_f (CH₄)

∆H_c2 = ∆H_c(C) + 2∆H_c(H₂)

∆H_c1 = ∆H_c(CH₄)

So:

∆H_f(CH₄)        = {∆H_c(C) + 2∆H_c (H₂)} - {∆H_c (CH₄)}

= -393 + 2(-286) - (-890)

=-75 kJ mol^-1

Enthalpy changes using formation data

• Sometimes it is necessary to use enthalpy change of formation to work out the enthalpy change of combustions. 

∆H_f1 = ∆H_f2 + ∆H_c

• The Enthalpy change from the elements in their standard states to the products is equal to the formation energy of the products plus the Enthalpy change from the elements in their standard states to the reactants.

To find out the Enthalpy change using Heats of combustion:

1.      Start with an equation to represent the energy change.

2.      Using the formation data complete a Hess law cycle.

3.      Balance the cycle and add symbols representing ∆H₁ ∆H₂ and ∆H_3.

4.      Remember to get the direction of change correct (arrows go form elements in standard states to the reactants and products).

5.      Use Hess's law to find the relationships between the enthalpy changes and rearrange to find the value wanted.

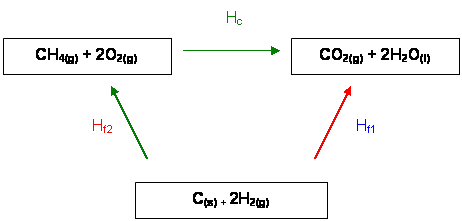
Example:

Find the enthalpy change for the following reaction:

CH_4(g) + 2O_2(g) CO_2(g) + 2H₂O_(l)

∆H_f1 = ∆H_f2 + ∆H_c

∆H_c = ∆H_c (C) + ∆H_f (CO_2(g)) + 2∆H_f (H₂O_(l))

∆H_f2 = ∆H_f2(CH_4(g))

∆H_f1 = ∆H_f2 + ∆H_c

So ∆H_c               = ∆H_f1 - ∆H_f2

                                = ∆H_f (CO_2(g)) + 2∆H_f (H₂O_(l)) - ∆H_cf(CH_4(g))

                                    =   -394       +    - 572       -     -75

                                    =  -891 KJ mol^-1

Useful books for revision: